2023年02月01日
2023新年度生、募集開始のお知らせ!
まだまだ寒い日が続きますが、
春に向けて、動き出しましょう!!
文字だらけの地味な広告になってしまいましたが、
その分、気持ちがこもった広告です(^^)/
下記のサムネイルをクリックすると拡大してご覧になれます!




ご不明な点などは、メールやお電話で、お気軽にお問合せ下さい。
春に向けて、動き出しましょう!!
文字だらけの地味な広告になってしまいましたが、
その分、気持ちがこもった広告です(^^)/
下記のサムネイルをクリックすると拡大してご覧になれます!




ご不明な点などは、メールやお電話で、お気軽にお問合せ下さい。
Posted by planus at
19:06
│Comments(0)
│好奇心を育てるには│塾案内│合格実績│お問合せ│小学校低学年のための「curio」コース│塾のタイプ(塾選びのヒント)│学校と塾~さまざまな誤解を巡って~│生徒募集!
2022年09月20日
2学期の募集状況
いつの間にか秋、今年も残り3か月と気づいて、
びっくりしています。
おかげさまで、一部のクラスが定員となりましたので、
本年度の募集を一旦停止させて頂きます。
小学生(curioコース、基礎トレクラス)
中3生(グループレッスン)
高校生(小人数個別レッスン)
松本クラス(全学年)
以上のクラスは募集は停止になります。
他に、中1生(グループレッスン)の募集が、
残り若干名となります。
引き続き、よろしくお願い致します<(_ _)>
びっくりしています。
おかげさまで、一部のクラスが定員となりましたので、
本年度の募集を一旦停止させて頂きます。
小学生(curioコース、基礎トレクラス)
中3生(グループレッスン)
高校生(小人数個別レッスン)
松本クラス(全学年)
以上のクラスは募集は停止になります。
他に、中1生(グループレッスン)の募集が、
残り若干名となります。
引き続き、よろしくお願い致します<(_ _)>
2022年07月23日
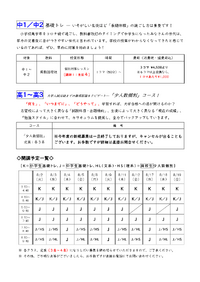
夏塾2022「予約状況」
7/23現在の予約状況です。
キャンセルが出る場合もあるので、
詳細は直接お問い合わせください。
(メール(SNS経由含む)、大歓迎です)
※中3グループレッスンは満員のため、募集を停止しております<(_ _)>
↓のサムネイルをクリックしてご確認ください<(_ _)>

キャンセルが出る場合もあるので、
詳細は直接お問い合わせください。
(メール(SNS経由含む)、大歓迎です)
※中3グループレッスンは満員のため、募集を停止しております<(_ _)>
↓のサムネイルをクリックしてご確認ください<(_ _)>

2022年07月04日
2022年02月04日
学習塾激戦区「松本」
数多の学習塾が立ち並ぶ松本市、
時に不便なことも起こるオンライン授業、
それでもなお、茅野市の端っこにある、
プラナスを選んでくれるみなさんが増えてきました。
「たくさんの塾を調べたけど、先生のような考え方で、
算数、数学を教えてくれる先生は松本にはいなかった」
(たぶん、諏訪圏にもいないと思う)
2年前の「ママ算数inまつもと」以来、
何度も、そんなラブコール(古っ笑)を頂きながら、
なかなか、決心がつきませんでしたが・・・
いよいよ、新年度、松本に行ってみまーす(^^)/
さて、さて、どんな結果が待ち受けているでしょうか?
注:もちろん、茅野からいなくなるということではないです。
こちらも、新年度生募集中ですので(^^)

時に不便なことも起こるオンライン授業、
それでもなお、茅野市の端っこにある、
プラナスを選んでくれるみなさんが増えてきました。
「たくさんの塾を調べたけど、先生のような考え方で、
算数、数学を教えてくれる先生は松本にはいなかった」
(たぶん、諏訪圏にもいないと思う)
2年前の「ママ算数inまつもと」以来、
何度も、そんなラブコール(古っ笑)を頂きながら、
なかなか、決心がつきませんでしたが・・・
いよいよ、新年度、松本に行ってみまーす(^^)/
さて、さて、どんな結果が待ち受けているでしょうか?
注:もちろん、茅野からいなくなるということではないです。
こちらも、新年度生募集中ですので(^^)

2022年01月31日
2021年11月29日
冬期講習会のお知らせ
ようやく落ち着いてきた日常に、
新しい変異株のニュースが飛び込んできました。
何とか、水際で食い止めてほしいところですが、
どんな状況になっても慌てないよう、
今のうちに準備できることをしておくことも重要だと思います。
もちろん、「学び」についても同様です。
さて、今回は冬期講習会のご案内です。
ご質問、お問合せはブログのメールからも可能です。
お気軽にお問合せください




新しい変異株のニュースが飛び込んできました。
何とか、水際で食い止めてほしいところですが、
どんな状況になっても慌てないよう、
今のうちに準備できることをしておくことも重要だと思います。
もちろん、「学び」についても同様です。
さて、今回は冬期講習会のご案内です。
ご質問、お問合せはブログのメールからも可能です。
お気軽にお問合せください





2021年07月05日
「夏塾!」~2021~
プラナスの夏期講習会、「夏塾!」
募集をスタートします
ご質問、お問い合わせ等は、
このブログのコメント欄、メール、Facebook、Instagram。。。などからも受け付けます!




募集をスタートします

ご質問、お問い合わせ等は、
このブログのコメント欄、メール、Facebook、Instagram。。。などからも受け付けます!




Posted by planus at
17:57
│Comments(0)
│好奇心を育てるには│塾でのあれこれ│塾案内│合格実績│代表紹介│高校生クラス│塾のタイプ(塾選びのヒント)│学校と塾~さまざまな誤解を巡って~│生徒募集!
2021年06月28日
小6「分数のわり算」の文章題は分数で解けないのが普通?(後編)
さて、前回のブログの後編です。
よろしければ、前回のブログをご覧になってからお進みください。
きっかけとなったのは↓の問題でした。

小中学校のカリキュラムは「計算」から入って、
その計算を利用した「文章題」に移るという進行が一般的です。
でも、よく考えてみると、おかしくないですか?
解決したい問題があって、
そのために必要な道具を用意する方が自然だと思いませんか?
例えば、
野球をやりたいのかサッカーをやりたいのか決まってもいない小さな子どもに、
「いずれ、役に立つはずだから」と筋トレだけやらせようと思いますか?
前回、取り上げた文章題、問題文の中には分数は出てきません。
塾に通っている清陵生の解答はこうでした・・・
60:80=X:240
3:4=X:240
4X=720
X=180
よって180㎥
※「本当は最初の式で80の3倍が240だから、
そのまま60も3倍して180で良くない?」とアドバイスしておきました。
ある中学3年生はこうでした。
240÷80=3
3×60=180
塾に通う小6生の、今回の考え方と同じですね。
時間の単位換算ができて、整数のわり算とかけ算が使えれば、
シンプルに解けるはずの問題を、
なぜ、
「その単元だから」という理由で無理やり「分数のわり算」で解かなければいけないのか?
しかも、
仮に、「分数のわり算」の方が、この文章題を解くのに有利で分かりやすい解法だとしたら、
中学生や高校生も「分数のわり算」で解く子が多くなるはずではないでしょうか?
もう一人の甲陵に通う高校生が、こんなことを言ってくれました。
「文章題から考えてないですね」
さすが、プラナスに長年通っている生徒!(自画自賛)
そうなんです、計算のやり方だけ練習させて(しかも、あまり訳もわからずに)、
その後、体裁を整えるために、「さぁ、分数のわり算を使って文章題を解きましょう」となるので、
なぜ、その文章題を解くために「分数のわり算」が適切なのか、
本当に、それが最善の解き方なのかと考えることなく、
その場は、何となく数字を見つけて、
分数のわり算で解くという「一種の公式」に当てはめているだけになっているのです。
結果として、いずれ、複数の単元をミックスして文章題を出題されると、
「どの道具を使えばいいのかわからない。計算は得意だけど、文章題はキライ。」という子どもが
どんどん増えてしまうのです。
高校生が代弁してくれたように、
算数・数学にとっての基礎力とは「計算」ではなくて、
「文章題」の理解や概念の理解だということに気づいているかどうかが、
算数・数学を好き(得意)になるかどうかの大きな分かれ道なのです。
よろしければ、前回のブログをご覧になってからお進みください。
きっかけとなったのは↓の問題でした。

小中学校のカリキュラムは「計算」から入って、
その計算を利用した「文章題」に移るという進行が一般的です。
でも、よく考えてみると、おかしくないですか?
解決したい問題があって、
そのために必要な道具を用意する方が自然だと思いませんか?
例えば、
野球をやりたいのかサッカーをやりたいのか決まってもいない小さな子どもに、
「いずれ、役に立つはずだから」と筋トレだけやらせようと思いますか?
前回、取り上げた文章題、問題文の中には分数は出てきません。
塾に通っている清陵生の解答はこうでした・・・
60:80=X:240
3:4=X:240
4X=720
X=180
よって180㎥
※「本当は最初の式で80の3倍が240だから、
そのまま60も3倍して180で良くない?」とアドバイスしておきました。
ある中学3年生はこうでした。
240÷80=3
3×60=180
塾に通う小6生の、今回の考え方と同じですね。
時間の単位換算ができて、整数のわり算とかけ算が使えれば、
シンプルに解けるはずの問題を、
なぜ、
「その単元だから」という理由で無理やり「分数のわり算」で解かなければいけないのか?
しかも、
仮に、「分数のわり算」の方が、この文章題を解くのに有利で分かりやすい解法だとしたら、
中学生や高校生も「分数のわり算」で解く子が多くなるはずではないでしょうか?
もう一人の甲陵に通う高校生が、こんなことを言ってくれました。
「文章題から考えてないですね」
さすが、プラナスに長年通っている生徒!(自画自賛)
そうなんです、計算のやり方だけ練習させて(しかも、あまり訳もわからずに)、
その後、体裁を整えるために、「さぁ、分数のわり算を使って文章題を解きましょう」となるので、
なぜ、その文章題を解くために「分数のわり算」が適切なのか、
本当に、それが最善の解き方なのかと考えることなく、
その場は、何となく数字を見つけて、
分数のわり算で解くという「一種の公式」に当てはめているだけになっているのです。
結果として、いずれ、複数の単元をミックスして文章題を出題されると、
「どの道具を使えばいいのかわからない。計算は得意だけど、文章題はキライ。」という子どもが
どんどん増えてしまうのです。
高校生が代弁してくれたように、
算数・数学にとっての基礎力とは「計算」ではなくて、
「文章題」の理解や概念の理解だということに気づいているかどうかが、
算数・数学を好き(得意)になるかどうかの大きな分かれ道なのです。
Posted by planus at
22:06
│Comments(0)
│好奇心を育てるには│塾でのあれこれ│高校生クラス│小学校低学年のための「curio」コース│塾のタイプ(塾選びのヒント)│学校と塾~さまざまな誤解を巡って~│生徒募集!│ママが楽しむ算数講座│ガリレオの望遠鏡で八ヶ岳の星空を見上げてみる
2021年02月26日
3月からは「新学年」!
みなさんは、どんな塾、教材を探していますか?
ある体験授業に来た子どもに
「余りのある割り算はできる?」と質問すると。
「できるよ!」という答えがかえってきました。
確かに「14÷6=2あまり2」とできていました。
そこで、もう1つ、
「この答(商)の『2』と、あまりの『2』は、どう違うの?」と質問しました。
すると、
「え!?『2』と『2』は同じでしょ?」と不思議そうに答えてくれました。
これは単純作業のように「計算ドリル」ばかりを繰り返しこなして、
機械的に解法や公式を丸暗記してきた子どもに多い症状です。

そして「紙のプリント」であっても、「AI搭載のタブレット教材」であっても、
「本質的には同じこと」が起こりえます。
お子さんの学びが「少しうまくいっていないな」と感じている親御さんは、
今、使っている教材や、通っている塾が「何を目指し、何を重視しているか」を再確認してみてはいかがでしょうか?
↓こちらの記事も参考になると思います。(リンク先にジャンプします)
「数学嫌いの若者」が生みだされ続ける根本原因(東洋経済on line)
以下、上記の記事本文より引用~
小学校の算数教育で必ず登場することに「九九」がある。3×4=12の「サンシジュウニ」ならば、3+3+3+3=12を示した後に暗記させるものである。ところが、困った指導が一部で行われて、3×4=12のような意味を示す前に九九を全部暗唱させていたのである。
ある体験授業に来た子どもに
「余りのある割り算はできる?」と質問すると。
「できるよ!」という答えがかえってきました。
確かに「14÷6=2あまり2」とできていました。
そこで、もう1つ、
「この答(商)の『2』と、あまりの『2』は、どう違うの?」と質問しました。
すると、
「え!?『2』と『2』は同じでしょ?」と不思議そうに答えてくれました。
これは単純作業のように「計算ドリル」ばかりを繰り返しこなして、
機械的に解法や公式を丸暗記してきた子どもに多い症状です。

そして「紙のプリント」であっても、「AI搭載のタブレット教材」であっても、
「本質的には同じこと」が起こりえます。
お子さんの学びが「少しうまくいっていないな」と感じている親御さんは、
今、使っている教材や、通っている塾が「何を目指し、何を重視しているか」を再確認してみてはいかがでしょうか?
↓こちらの記事も参考になると思います。(リンク先にジャンプします)
「数学嫌いの若者」が生みだされ続ける根本原因(東洋経済on line)
以下、上記の記事本文より引用~
小学校の算数教育で必ず登場することに「九九」がある。3×4=12の「サンシジュウニ」ならば、3+3+3+3=12を示した後に暗記させるものである。ところが、困った指導が一部で行われて、3×4=12のような意味を示す前に九九を全部暗唱させていたのである。